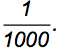Harvard Medical School Test

Introduction

“We developed a test for a disease. The false negative rate is zero (“sensivity”), the false positive rate is (“specifity”) and the incidence of the disease in the population is ”

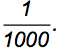“What is the probability that a randomly selected person has the disease?”

This question was posed at the Harvard Medical School to staff and students alike (see ), but similar questions are surely part of many Statistics introductory courses as well.

Sampling

We solve the problem by sampling.

We denote with “0” a person in the population which does not have the disease under question. We denote with “1” a person which does have the diesease.

Define the size of the population, the prevalence of the disease in the population and the false positive rate of the test:

Generate the population to draw from:

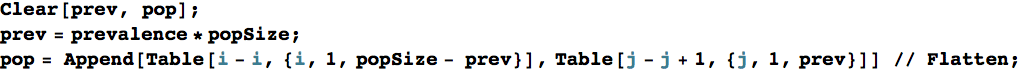
Define a predicate for the result of the test, person ∈{0,1}, ‘True’ if the test(!) delivers a positive test result, ‘False’ otherwise:

Define a predicate whether a person really has the disease:

Do a Monte Carlo simulation to find an estimate of the probability.

Bayes’ Rule

It is instructive to solve for this conditional probability analytically.

To do this, we need to apply Bayes’ rule:

H denotes the hypothesis and E the corresponding evidence. Note that this is the form as derived by Thomas Bayes himself.

First Implementation

Let’s write a function which implements this rule.

What are the arguments for our problem?
H = “The person has the disease.”,
E = “The test for the person is positive.”,
P(H) = ,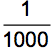
P(¬H) = ,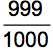
P(EH) = 1 [because the test finds the disease always (= 1- false neg. rate)],
P(E¬H) = ( = false positive rate),
P(E) = P(EH) *P(H) + P(E¬H)*P(¬H) = 1*.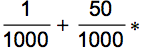

Second Implementation

We follow the approach as given in stackoverflow:

Third Implementation

We follow the second approach as given in stackoverflow:

Bibliography

1. Casscells, Ward and Schoenberger, Arno and Graboys, Thomas B., Interpretation by Physicians of Clinical Laboratory Results. New England Journal of Medicine, 1978.

Created with Wolfram Mathematica 9.0